递归问题

2019-01-07

学习《数据结构与算法之美》时的笔记。

如何理解递归

例：领导分配给你一个任务量为n的任务，你做了一部分，然后把剩下的n-1分配给别人，别人又做了一部分，把剩下的n-2分配给了另一个人，直到最后一个人，做了一部分，然后把任务完成返回给他上一个人。

这个任务下发的过程叫递，任务返回的过程叫归。

基本上，所有的递归问题都可以用递推公式来表示，上面这个例子，递推公式表示为：f(n)=f(n-1)+1 其中，f(1)=1。

上述递归问题的代码表示如下：

int f(int n) 
{
  if (n == 1) 
      return 1;
  return f(n-1) + 1;
}

递归需要满足的条件

1）一个问题可以分解为几个字问题的解

2）这个问题与分解之后的字问题，除了数据规模不同，求解思路完全一样

3）存在递归终止条件

举个栗子：

树的定义是一种递归形式的定义，对于树的前序遍历，有：

void PreOrder(struct TreeNode *root)
{
    if (root == NULL)	// 递归的终止条件
        return;
    
    /* 处理root */
    PreOrder(root->left);	// 递推，左子树
    PreOrder(root->right);	// 递推，右子树
}

在一些树的相关题目中，以这种递推的思想来处理问题还是比较方便的。

递归代码如何实现

写递归代码最关键的是写出递推公式，找到终止条件。

青蛙跳台阶问题：

假设有n个台阶，每次青蛙可以跳1个台阶或者2个台阶，请问走完这n个台阶有多少种走法？

例如：有7个台阶，可以2，2，2，1上去，也可以1，2，1，1，2这样上去，总之走法很多，如何编程实现呢？

分析：根据第一步走法把所有走法分为2类，第一类：第一步走了1个台阶，第二类：第一步走了2个台阶。所以n个台阶的走法 =（先走1个台阶后，n-1个台阶的走法）+（先走2个台阶后，n-2个台阶的走法）

用递推公式表示就是：

f(n) = f(n-1)+f(n-2)

递推的终止条件：

当有一个台阶时，不需要再继续递归，只有一中走法。

当有两个台阶时，可以每次走1个台阶，走两次，也可以一次两个。

当有三个台阶时，就分解为有一个台阶和两个台阶的问题了。

所以有：

int f(int n) 
{
  if (n == 1) 
      return 1;
  if (n == 2) 
      return 2;
  return f(n-1) + f(n-2);
}

人脑几乎没办法把整个递归的过程一步一步想清楚，所以很多时候，我们只需要把它抽象成一个递推公式，不用想一层一层的调用关系，这些交给计算机来做就好了。

要注意栈溢出！

如果递归求解的数据规模很大，调用层次很深，就会有栈溢出的发生。

我的一次栈溢出的经历：在练习用递归模拟strlen函数功能时，如下代码：

int my_strlen(char *str)
{
    if(*str == '\0')
        return 0;
    return 1 + my_strlen(str++);
}

这里传进去的始终是str，所以没有终止的一直压栈，导致栈溢出。

解决栈溢出的方法：

1）限制递归深度

这种做法并不能完全解决问题，因为最大允许的递归深度和当前线程剩余的栈空间大小有关，事先无法计算，如果实时计算，代码过于复杂，影响可读性。所以对于最大深度比较小的情况，如10、50，就可以用这种方法，否则这种方法并不是很实用。

2）在堆区模拟系统的工作栈

如果需要可以采用这种方法。

警惕重复计算

以青蛙跳台阶的问题为例：

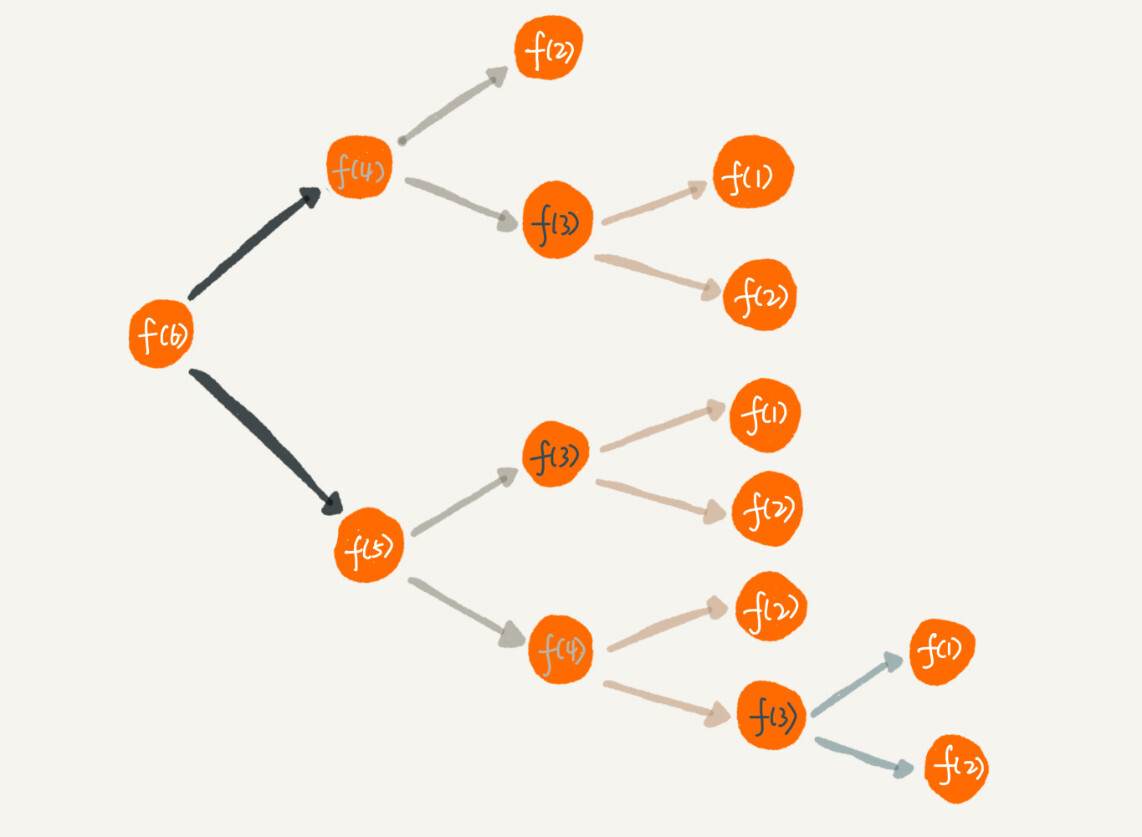
图片引用自极客时间

从图中可以看到：想要计算f(5)，需要先计算f(4)和f(3)，而f(4)还需要计算f(3)，因此，f(3)被重复计算了多次，这就是重复计算问题！

还有个例子：递归方法求第n个斐波那契数，也会有同一n重复计算多次的现象。

当计算第50个斐波那契数时，f(3)被计算了上亿次，这个计算花了10分钟左右！

重复计算的解决方法：

为了避免这种重复计算带来的负面开销，可以通过引入散列表来保存已经求过的f(k)。当递归调用到f(k)时，先看下是否求解过了，如果是直接从散列表中取这个值，就不需要再次计算了。

递归代码改写为非递归代码

递归有利有弊，递归的问题不仅仅就上面说的重复计算和栈溢出，递归的空间复杂度有时也比较高。

如果用递归方法求第n个斐波那契数，时间开销比较大，还是用循环比较好。

对于上文中两个例子改写如下：

/* 领导分配工作 */
int f(int n) 
{
  int ret = 1;
  for (int i = 2; i <= n; ++i) 
  {
    ret = ret + 1;
  }
  return ret;
}

/* 青蛙跳台阶问题 */
int f(int n) 
{
  if (n == 1) 
      return 1;
  if (n == 2) 
      return 2;
  
  int ret = 0;
  int pre = 2;
  int prepre = 1;
  for (int i = 3; i <= n; ++i) 
  {
    ret = pre + prepre;
    prepre = pre;
    pre = ret;
  }
  return ret;
}

这种思路其实是将递归改成了“手动”递归，本质没有变，增加了实现难度。

经典递归问题

在n个球中，任意取m个(不放回)，求有多少种取法

#include <stdio.h>

int f(int n, int m)
{
    if (n<m)    // 3个球取4个出来 显然是0种取法
    {
        return 0;
    }
    if (m==0)   // 3个球取0个出来 有1种取法
    {
        return 1;
    }
    if (n==m)   // 3个球取3个出来 有1种取法
    {
        return 1;
    }
    return f(n-1, m-1) + f(n-1, m);
}

int main(int argc, const char * argv[])
{
    int k = f(5, 3);
    printf("%d\n", k);
    
    return 0;
}

求n个元素的全排列

// abc acb bac bca cab cba
#include <stdio.h>

void f(char data[], int length, int cur)
{
	if(cur==length)
		printf("%s\n", data);
	for(int i=cur; i<length; i++)
	{
		{	// 试探
			char tmp = data[i];
			data[i] = data[cur];
			data[cur] = tmp;
		}

		f(data, length, cur+1);

		{	// 回溯
			char tmp = data[i];
			data[i] = data[cur];
			data[cur] = tmp;
		}
	}
}

int main()
{
	char data[] = "abcd";
	int length = sizeof(data)/sizeof(data[0]) - 1;
	//printf("%d\n",length);
	f(data, length, 0);
	return 0;
}

两个串的最大公共子序列的长度

// 可解!

#include <stdio.h>
#include <string.h>

int MAX(int a, int b)
{
    return a>b?a:b;
}

int f(char *s1, char *s2)
{
    if (strlen(s1)*strlen(s2) == 0)
    {
        return 0;
    }
    if (s1[0] == s2[0])
    {
        return f(s1+1, s2+1) + 1;
    }
    else
    {
        return MAX(f(s1+1, s2), f(s1, s2+1));
    }
}

int main(int argc, const char * argv[])
{
    char *s1 = "abc";
    char *s2 = "xbacd";
    
    int ret = f(s1, s2);
    printf("%d\n", ret);
    
    return 0;
}

字符串反转

// 反转串
// 例如：abc  ->  cba

#include <stdio.h>
#include <string.h>

void ReverseString(char *p)
{
    int length = strlen(p);
    if(length <= 1)
    {
        return;
    }
    else
    {
        char tmp = p[0];
        p[0] = p[length-1];
        p[length-1] = '\0';
        ReverseString(p+1);
        p[length-1] = tmp;
    }
}

int main()
{
	char p[] = "abcd";
    ReverseString(p);
    printf("%s\n", p);
	return 0;
}

组合问题

// 组合问题
// 3个A 2个B可以组成多少 种 排列
// 如：AAABB AABBA等

#include <stdio.h>

// m个A n个B
int f(int m, int n)
{
    if(m == 0 || n == 0)
    {
        return 1;
    }
    // 假设首位置为A，则剩下m-1个A和n个B的组合问题 + 首位置为B...
    return f(m-1, n) + f(m, n-1);
}

int main()
{
    printf("%d\n", f(3, 1));
    return 0;
}

杨辉三角

// 杨辉三角
// 计算第m层第n个元素

/*
 1
 1 1
 1 2 1
 1 3 3 1
 1 4 6 4 1
 1 5 10 10 5 1
 */

#include <stdio.h>

int f(int m, int n)
{
    if(n == 0)
    {
        return 1;
    }
    if(m == n)
    {
        return 1;
    }
    return f(m-1, n) + f(m-1, n-1);
}

int main()
{
    int leval = 5;  // 第5行 0-5共6个元素
    for(int i=0; i<=leval; i++)
    {
        printf("%d ", f(leval, i));
    }
    printf("\n");
    return 0;
}

整数划分问题

// 整数划分问题
// n = 6
/*
 6
 5+1
 4+2,4+1+1
 3+3,3+2+1,3+1+1+1
 2+2+2,2+2+1+1,2+1+1+1+1
 1+1+1+1+1+1
 */

#include <stdio.h>

#define MAXSIZE 1024

// arr->缓冲，cur->当前位置
void f(int n, int arr[], int cur)
{
    if(n<=0)
    {
        for(int i=0; i<cur; i++)
        {
            printf("%d ", arr[i]);
        }
        printf("\n");
        return;
    }
    
    for(int i=n; i>0; i--)
    {
        if(cur>0 && i>arr[cur-1])
        {
            continue;
        }
        arr[cur] = i;
        f(n-i, arr, cur+1);
    }
}

int main()
{
    int arr[MAXSIZE] = {0};
    f(6, arr, 0);
    return 0;
}

参考文章：《数据结构与算法之美》