此文是学习《数据结构与算法之美》时的笔记。
如何理解跳表
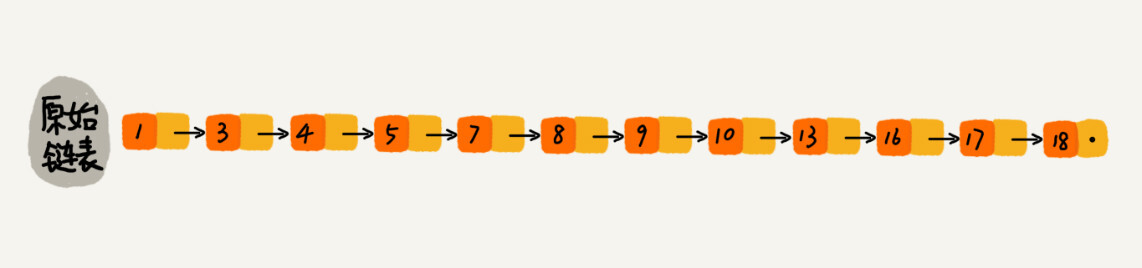
对于单链表来讲,即便链表中存储的数据是有序的,要查找某个数据,也只能从头到尾遍历链表。时间复杂度很高,为O(n)。
跳表,就可以提高查找效率。
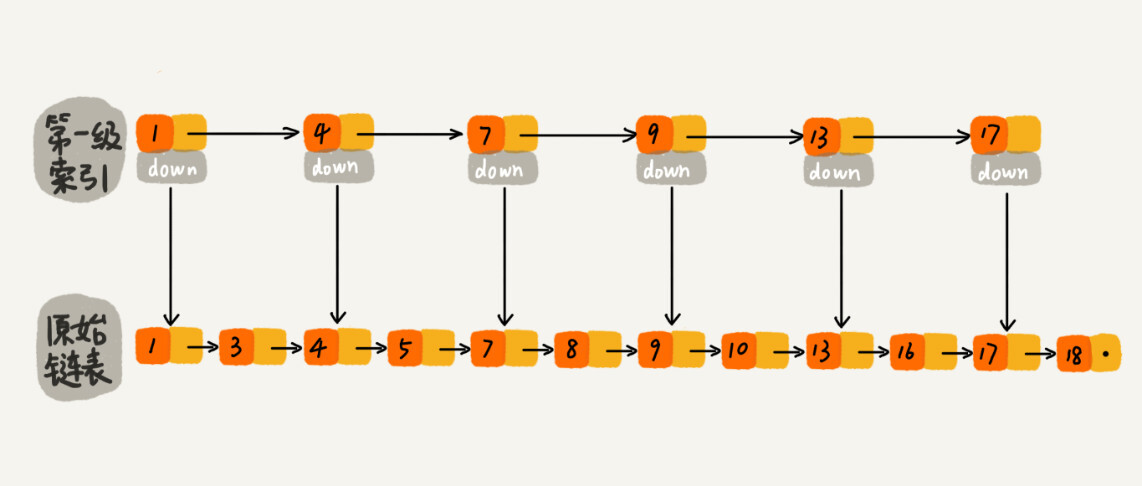
如上图,对链表建立一级索引,每两个结点提取一个结点到上一级,down表示down指针,指向下一级结点。
如果现在要查找值为16的结点,先在索引层遍历,13\le 16 \le17,通过13这个结点的down指针,下降到原始链表着一层,继续遍历,这个时候只需要再遍历2个结点,就可以找到目标。如果直接遍历原始链表,需要遍历10个结点,现在只需要遍历7个。
加了一层索引之后,查找的效率提高了,那再加一层会不会提升更多?
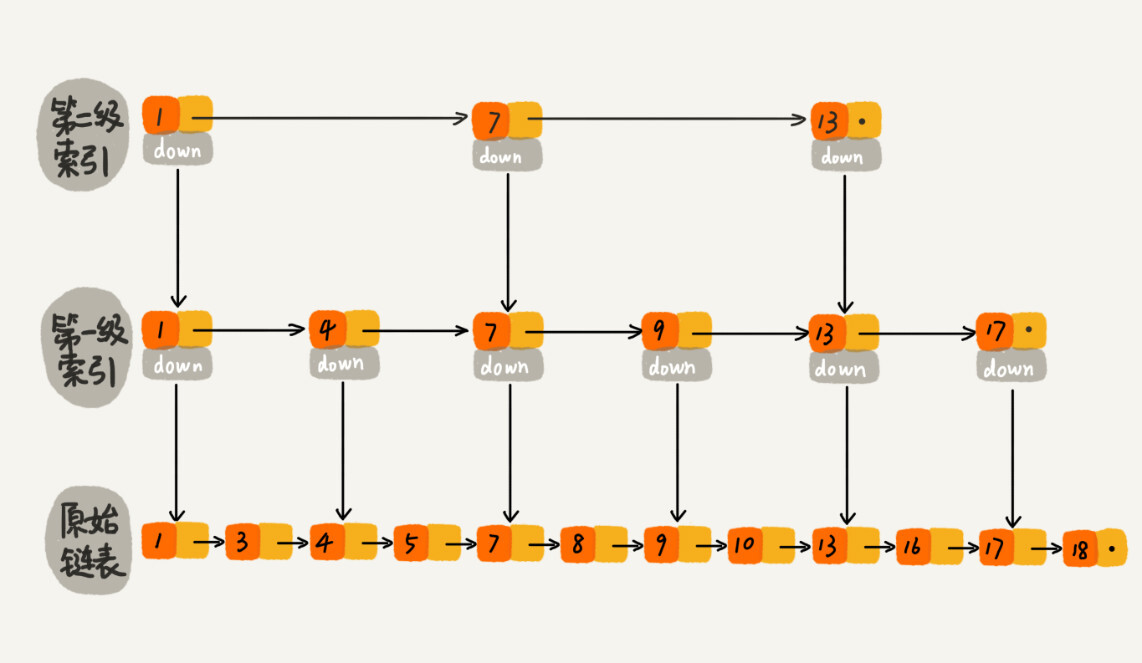
在加一层索引后,查找16就只需要遍历6个结点。
当数据规模大一点的时候,效率就很突出了。
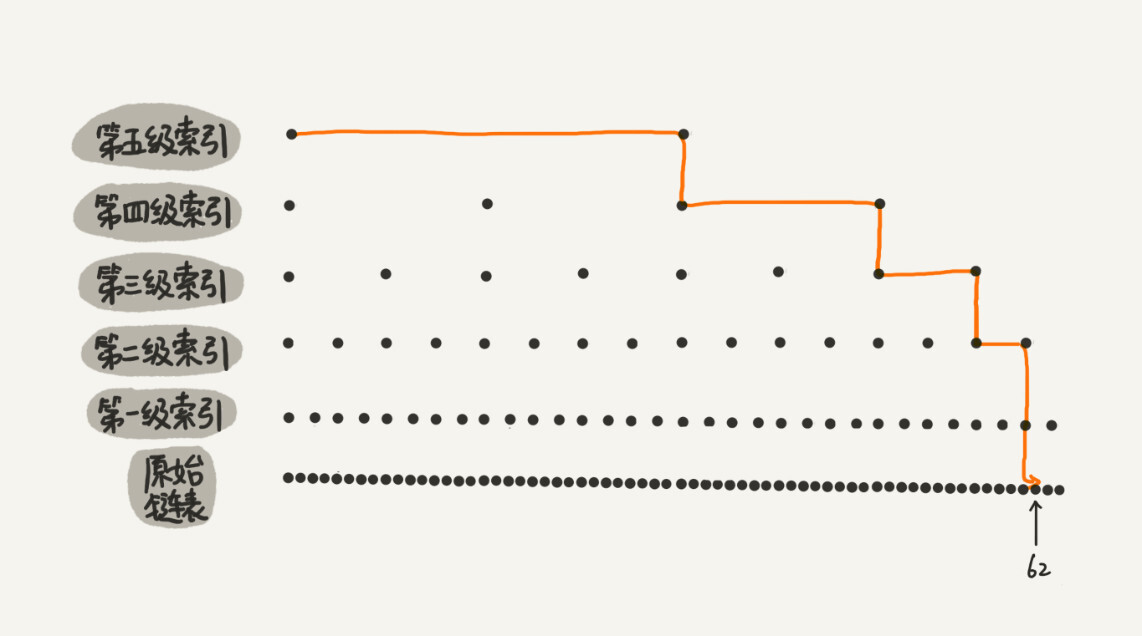
从上图中,查找62只需要遍历11个结点,所以当脸变长度n比较大时,比如1k、1w的时候,建立索引之后,效率提升就很明显!
跳表查找复杂度
时间复杂度
在单链表中查找一个数据的时间复杂度为O( n )。
在跳表中,每2个结点抽出一个结点作为上一级索引的结点,那第一级索引的结点个数(大约)为\frac {2}{n},第二级索引的结点个数(大约)是\frac n{4},第三级为\frac {n}{8},以此类推,第k级索引的结点个数是第k-1级索引的结点个数的\frac {1}{2},那第k级索引结点的个数就是\frac {n}{2^k}。假设索引有h级,最高级的索引有2个结点。所以有\frac {n}{2^h}=2,解得:h=\log_2n-1。如果包含原始链表着一层,整个跳表的高度就是\log_2n。在跳表中查询某个数据的时候,如果每一层需要遍历m个结点,那么跳表中查询一个数据的时间复杂度为O(m\times\log n)。
按照上面这种索引结构,m=3,也就是说每一级索引都最多只需要遍历3个结点。解释:假设要查找的数据是x,在第k级索引中,遍历到y结点之后,发现x大于y,小于后面的结点z,所以通过down指针,从第k级索引下降到k-1级。在第k-1级索引中,y和z之间只有3个结点(包括y和z),索引在k-1级索引中最多需要遍历3个基点,依次类推,每一级索引都最多只需要遍历3个结点。
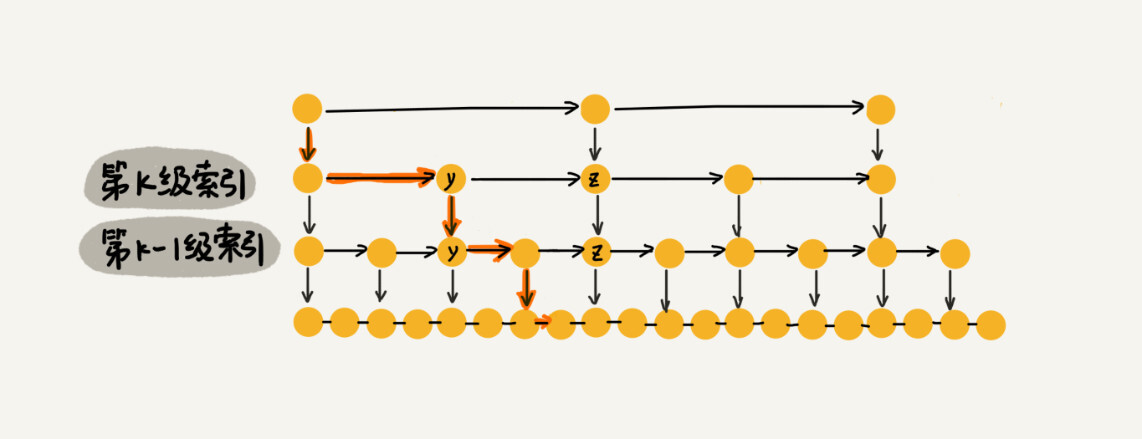
所以,在跳表中查询任意数据的时间复杂度为O(\log n)。这个复杂度和二分查找是一样的。
空间复杂度
跳表通过空间换时间,是不是很浪费内存?
假设原始链表的大小为n,每两个结点抽一个,第一级索引大约有\frac {n}{2}个结点,第二级索引大约有\frac {n}{4}个结点,以此类推,每上升一级就减少一半,直到剩下两个结点,等比数列。求和得到最终耗费n-2。所以跳表的空间复杂度是O( n)。也就是说,数据规模越大,跳表索引耗费的空间就越大。

每3个或者5个结点抽取一个作为索引,会不会更省内存?
每3个结点抽1个,等比数列\frac{n}{3}+\frac{n}{9}+\frac{n}{27}+…+9+3+1=\frac{n}{2}。空间复杂度还是O( n),但是比每2个结点抽取一个的构建方法减少了一半的索引存储空间。
实际上,在开发中,要处理的数据不一定是整数,原始链表中存储的有可能是很大的对象,而索引结点只需要存储关键值和几个指针,并不需要存储对象,所以当对象比索引结点大很多时,索引占用的额外空间就可以忽略了。
高效的动态插入和删除
跳表动态的插入、删除操作的时间复杂度为O(log n)。
插入操作
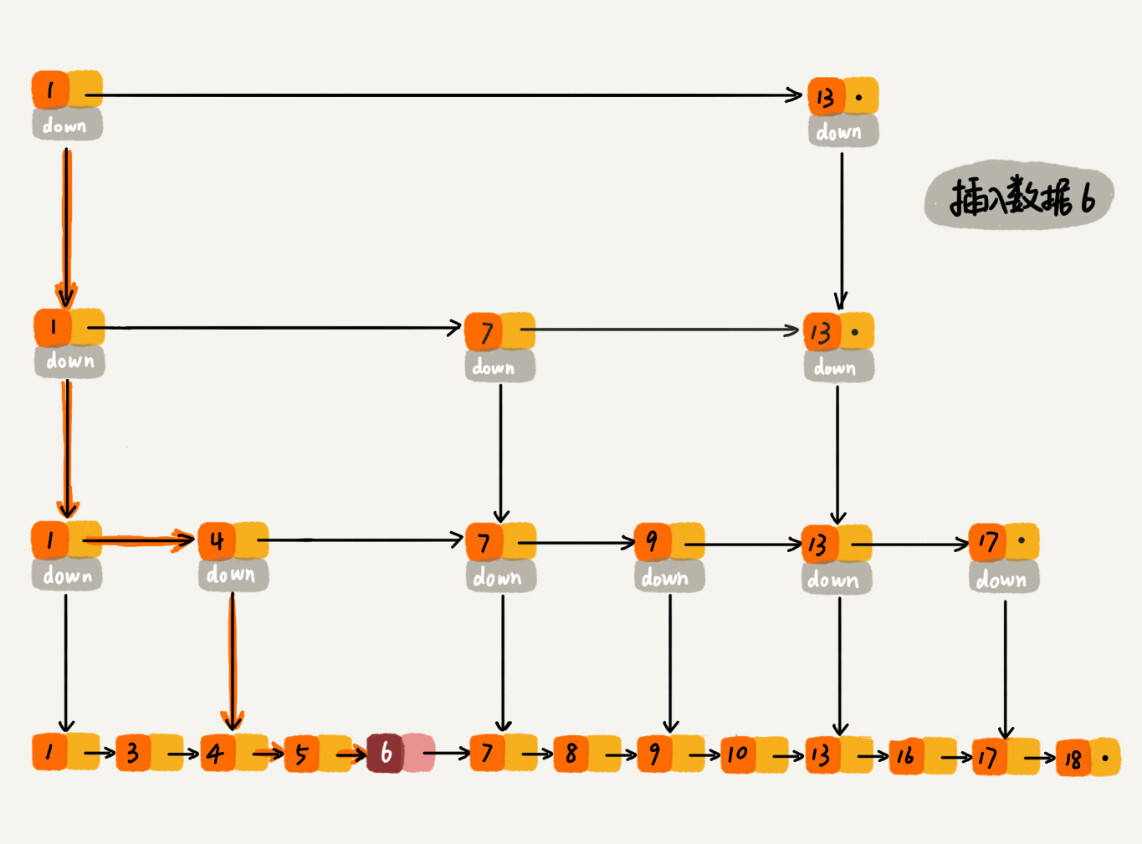
在链表中,只要找到了插入的位置,插入结点的时间复杂度是O( 1)。主要的时间花费在查找上,查找的时间复杂度是O( \log n)。
删除操作
删除操作中要注意!如果这个结点在索引中也有出现,除了删除原始链表中的,还要删除索引中的。因为单链表中的删除操作需要拿到要删除结点的前驱结点,然后通过指针操作完成。
跳表索引动态更新
如果不更新索引,就有可能出现某2个索引结点之间数据非常多的情况,极端情况下退化成单链表。
一般通过一个随机函数来决定将这个结点插入到哪几级索引中,比如,随机函数生成了K,那么就把这个结点添加到第一级至第K级索引中。
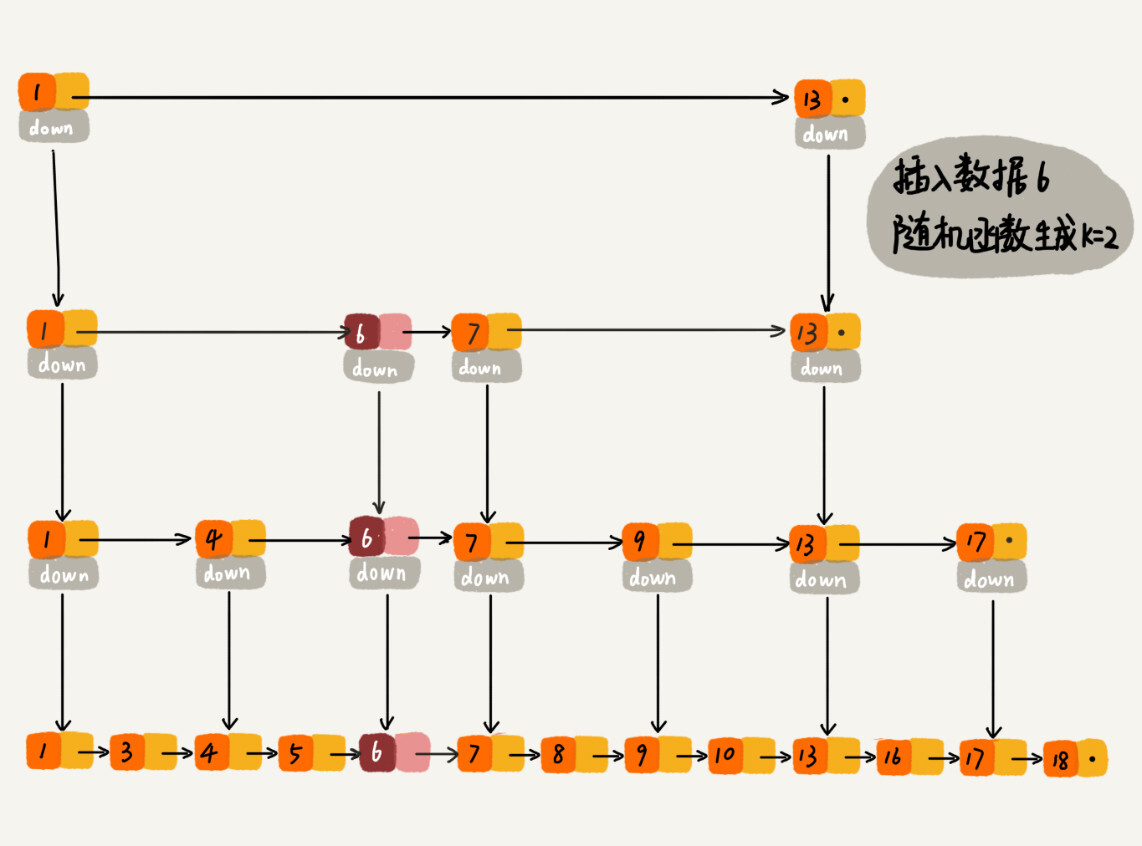
随机函数的选择很有讲究,从概率上来讲,能够保证跳表的索引大小和数据大小平衡性,不至于性能过度退化。
总结
跳表使用空间换时间,通过构建多级索引来提高查询效率,实现了基于链表的”二分查找”。
跳表是一种动态数据结构,支持快速的插入、删除、查找操作,时间复杂度都是O(\log n)。
跳表的空间复杂度是O(n)。不过跳表的实现非常灵活,可以通过改变索引构建策略,有效平衡执行效率和内存消耗。
数据结构与算法之美


